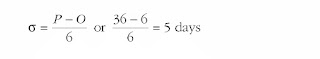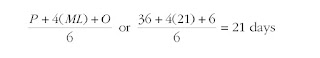Probability that activity
Activity A has a pessimistic (P) estimate of 36 days, a most likely (ML) estimate of 21 days, and an optimistic (O) estimate of 6 days. What is the probability that activity A will be completed in 16 to 26 days?
a. 55.70 percent
b. 68.26 percent
c. 95.46 percent
d. 99.73 percent
Answer: b. 68.26 percent
Step for calculate probability activity
First, compute the standard deviation:
Next, compute PERT expected time:
Finally, determine range of outcomes using 1σ:
21–5 = 16 days, and 21+5 = 26 days
Simply defined, 1σ is the amount on either side of the mean of a normal distribution that will contain approximately 68.26 percent of the population. [Planning]

![Probability that activity Activity A has a pessimistic (P) estimate of 36 days, a most likely (ML) estimate of 21 days, and an optimistic (O) estimate of 6 days. What is the probability that activity A will be completed in 16 to 26 days? a. 55.70 percent b. 68.26 percent c. 95.46 percent d. 99.73 percent Answer: b. 68.26 percent Step for calculate probability activity First, compute the standard deviation: First, compute the standard deviation: Next, compute PERT expected time: Next, compute PERT expected time: Finally, determine range of outcomes using 1σ: 21–5 = 16 days, and 21+5 = 26 days Simply defined, 1σ is the amount on either side of the mean of a normal distribution that will contain approximately 68.26 percent of the population. [Planning] Probability that activity Activity A has a pessimistic (P) estimate of 36 days, a most likely (ML) estimate of 21 days, and an optimistic (O) estimate of 6 days. What is the probability that activity A will be completed in 16 to 26 days? a. 55.70 percent b. 68.26 percent c. 95.46 percent d. 99.73 percent Answer: b. 68.26 percent Step for calculate probability activity First, compute the standard deviation: First, compute the standard deviation: Next, compute PERT expected time: Next, compute PERT expected time: Finally, determine range of outcomes using 1σ: 21–5 = 16 days, and 21+5 = 26 days Simply defined, 1σ is the amount on either side of the mean of a normal distribution that will contain approximately 68.26 percent of the population. [Planning]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEjIxtaTdfb8TGaf8GVi67OlgcfhJaNHopgsBii9ORs5MHUwgAGIyZUkcAXLizAled4AnSSZ6hP6_X0Bvc_YIH6nLnTw45eOVJa8m7cQXL6evkCCtRG7CjnlmzBgdJulR1YVhVY8jNTTmGdY/w640-h398/images+%25287%2529-01.jpeg)